Finite Dimensional Division Algebra
Let D be a finite dimensional division algebra over a finitely generated infinite field and let N C D X be a normal subgroup of finite index. It is well known that Dx is a principal right and left ideal ring and every two-sided ideal P in 7x has the form.
Https Doc Sagemath Org Pdf En Reference Algebras Algebras Pdf
The following are the only finite-dimensional associative algebras with division that is skew-fields over the real field.

Finite dimensional division algebra. I960 FINITE DIMENSIONAL CENTRAL DIVISION ALGEBRAS 29 2. For a division algebra D finite dimensional over its center ZDF it is a conjecture that CK1DCokerK1FK1D is trivial if and only if D11F with F a formally real Pythagorean. They lead to the definition of the Brauer group and to certain geometric objects the Brau er-Severi varieties.
This rules out most of the examples in VA4. Since every xin ZD is a root of the polynomial Xn-X ZD. Up to 10 cash back The beginning of investigations into finite-dimensional division algebras was made by Sir William Hamilton in 1843 when he discovered the algebra of real quaternions which rapidly led to diverse applications in physics and mechanics.
Let Gbe a finite group and Da division algebra faithfully G-graded finite dimensional over its center K where charK0. First we determine the structure of the primitive ideals and images of 7x. R then D R C or H.
Their definition gathers together all. In the second part Platonov and Yanchevskii survey the structure of finite-dimensional division algebras including an account of reduced K-theory. Consider the center ZD of D which is a field and contains a copy of K.
That is presumably also what you intend. The first contribution by Carter covers the theory of finite groups of Lie type an important field of current mathematical research. Finite-dimensional division algebras What about a vector space where you can multiply and divide vec-tors.
As Property 3 follows from the condition diamAH 4 this theorem con-. DEFINITIONA division algebra over a field F is an F-algebra A whose underlying ring is a division ring. In particular a finite-dimensional associative algebra without zero divisors is a skew-field.
ForexampleifD DQwhereQ isthe fieldofrationalnumbersthenforeverydiscretevaluationringV ofQ thereisa DubrovinvaluationringB ofD withB Q VindeedB hasthesepropertiesiff B isamaximalorderofV inD seethecommentsafterTh102below. If a finite-dimensional central division algebra D contains a maximal commutative subfield L which is a Galois extension of F then D is a cross product of L and G mathoprm Gal L F. It is a classical result by Kervaire and Milnor that every finite-dimensional real division algebra has dimension 124 or 8 with the most prominent examples being mathbbR mathbbC mathbbH and mathbbO.
Let eGdenote the identity element and suppose K0KDe the e-center of D contains ζnG a primitive nG-th root of unity where nGis the exponentof G. Let D be a finite-dimensional division algebra over the field K such that xnx for every xin D. If D is a division algebra with R in its center and D.
The real field the complex field and the skew-field of quaternions Frobenius theorem. Some mathematicians use division algebra over k to mean a finite dimensional k-algebra that is a division algebra and whose center equals k. For example prod-ucts like F F contain zero-divisors as do matrix algebras.
For infinite-dimensional division algebras the situation is quite different because a result of MokarLimonov states that such an algebra contains a free algebra in two variables. If H D x N satisfies Property 31 then N is open in Dx with respect to a nontrivial height one valuation of D. However other mathematicians make no such hypothesis about the center of the division algebra.
Proof of Theorem 1. Valuation Theory on Finite Dimensional Division Algebras 5 compriseamuchwiderclassofrings. Classification of Finite Dimensional Division R-algebras Theorem 8 Frobenius 1878.
Finite-dimensional division algebras over fields determine by the Wedderburn Theorem the semi-simple finite-dimensio nal algebras over a field. Up to 10 cash back Finite dimensional division algebras are as simple and spotless as a not necessarily commutative ring can be.

Axioms For Lattices And Boolean Algebras Pdf Algebra Mathematics Lattice
Normed Division Algebra In Nlab

Finite Dimensional Division Algebras Over Fields Nathan Jacobson Springer
Read Basic Algebra Ii Online By Nathan Jacobson Books
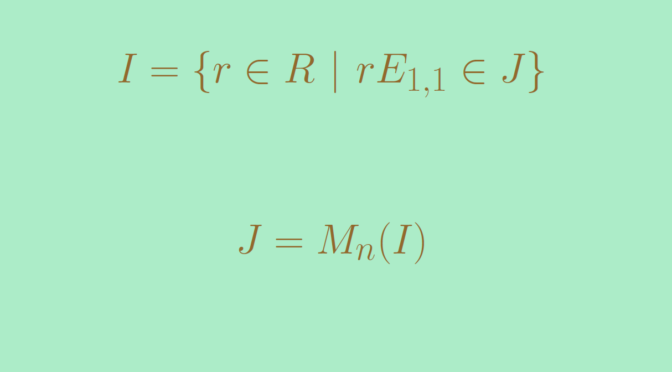
A Simple Ring Which Is Not A Division Ring Math Counterexamples

Division Algebra An Overview Sciencedirect Topics

Algebra Paper Retracted Because Of Questions About The Integrity Of The Mathematics Retraction Watch

Proof Of Wedderburn S Theorem Mathematics Stack Exchange

Algebraically Closed Field In A Division Ring Mathematics Stack Exchange

Multiply And Divide Functions Youtube Quadratics Mathematics Simplify

Solve One And Two Step Linear Equations Youtube Linear Equations Two Step Equations Inverse Operations

Pdf The Classification Of Real Division Algebras
Frobenius Theorem Bresar Theorem 1 4 Physics Forums

Sequence And Series Activity For Algebra 2 Sequence And Series Station Activities Algebra
Https Arxiv Org Pdf 1808 03172

Proof Of Wedderburn S Theorem Mathematics Stack Exchange
Read Basic Algebra Ii Online By Nathan Jacobson Books



